Réponse : 224000

Explications :

Le cercle jaune contient le nombre 40. Vers lui pointent deux flèches : l'une part du nombre 4 et l'autre d'un cercle bleu dont on ne connaît pas la valeur. La règle de l'énoncé demande que 40 = 4 × cette valeur, qui vaut donc 10. Voici le sapin avec le 10 inséré :

Vers le carré pointent deux nombres, le 7 et le 10 donc il contient 7 × 10 = 70.

Vers le cercle contenant 20 pointent trois flèches, la première part du 4, la seconde de l'hexagone, et la troisième d'un cœur : on a donc 20 = 4 × valeur de l'hexagone ×  valeur du cœur, si bien que la valeur de l'hexagone × la valeur du cœur = 20/4 = 5. Les seules façons d'écrire 5 comme un tel produit sont 5 = 1 × 5 et 5 = 5 × 1.

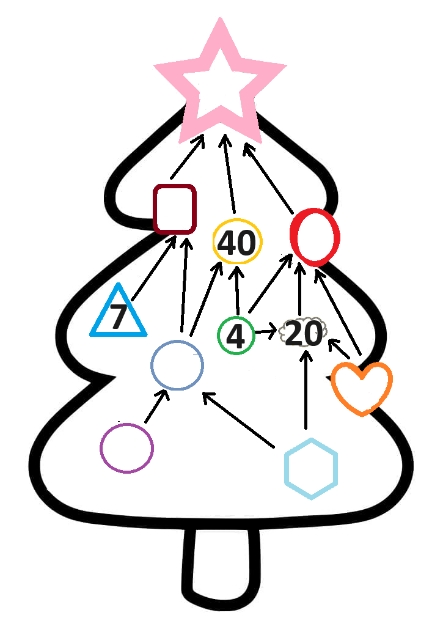
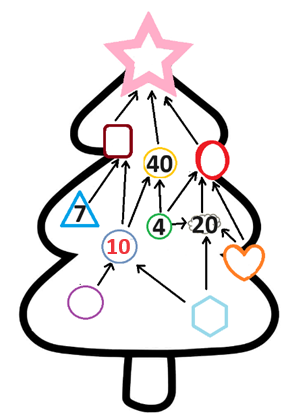
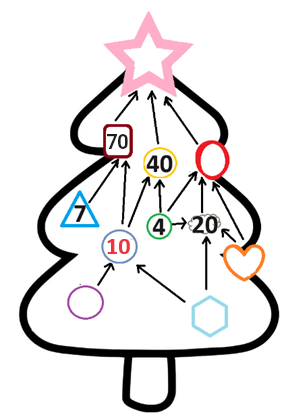
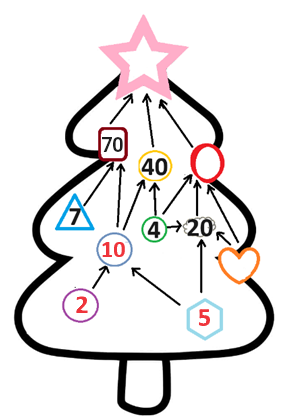
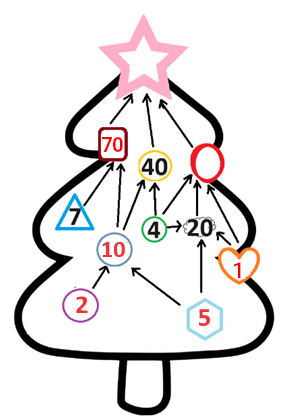
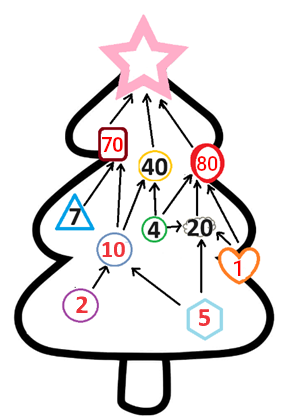
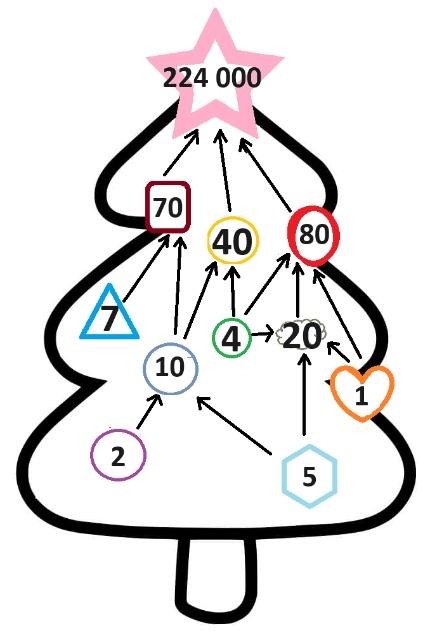
S'il y avait 1 dans l'hexagone, le cercle violet de gauche aurait la valeur 10, mais dans l'énoncé, on nous dit également que les boules portent des nombres différents et comme 10 est déjà présent dans le cercle bleu, il ne peut pas apparaître dans le cercle violet. Il y a donc 5 dans l'hexagone, et donc 2 dans le cercle violet et 1 dans le cœur.

Ainsi 20 = 4 × 5 × le nombre du coeur, donc ce nombre vaut 1.

Donc le cercle rouge contient 4 × 20 × 1 = 80

Et enfin dans l'étoile en haut du sapin, on a le produit 70 × 40 × 80 = 224 000.

Réponse : 3896

Explications :

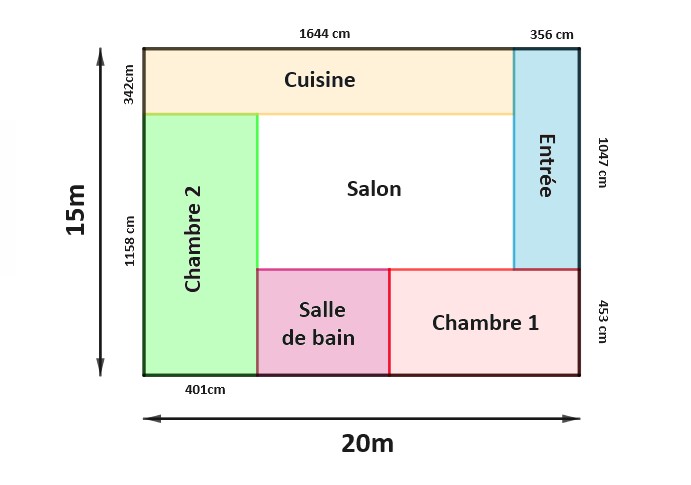
La salle de bain et la chambre n°1 ont une largeur en commun : elle mesure 453 cm qui est la seule valeur commune proposée par le lutin architecte. On peut donc assembler la salle de bain et la chambre 1, qui ont ensemble une longueur mesurant 1599 cm.

On en déduit les dimensions de la chambre 2 : sa largeur est la différence entre 20 m et 1599 cm, c’est-à-dire 401 cm, est sa longueur mesure donc 1158 cm. On peut ensuite trouver les dimensions de la cuisine et enfin de l’entrée.

On en déduit les dimensions du salon :

Longueur = 20 m – 401 cm – 356 cm = 1243 cm

Largeur = 15 m – 342 cm – 453 cm = 705 cm

2 × (1243 cm + 705 cm) = 3896 cm

Le périmètre du salon exprimé en cm est égal à 3896.

Réponse : 4997/71

Explications :

Notons \(x_1 < x_2 < ... < x_n\) les \(n\) éléments d’un ensemble de Noël rangés dans l’ordre croissant. La moyenne de tous ces éléments est : \[m = \frac{x_1 + x_2 + ... + x_n}{n}.\] La somme de tous les éléments est \[x_1 + x_2 + ... + x_n = m \times n.\] 1) Peut-on avoir une moyenne minimale avec un élément supérieur à 2512 ?

Si \(x_n\) est supérieur à 2512, alors en le supprimant on obtient l’ensemble \(\{x_1; x_2; ...; x_{n-1}\}\) qui est encore un ensemble de Noël et sa moyenne est \[m^{'} = \frac{x_1 + x_2 + ... + x_{n-1}}{n-1}= \frac{m \times n - x_n}{n-1} = \frac{m \times (n-1) +m -x_n}{n-1}= m + \frac{m-x_n}{n-1}.\] Comme \(x_n\) est supérieur à \(x_1, x_2, ...\), il est supérieur à la moyenne \(m\). Donc \(m-x_n\) est négatif et la moyenne \(m^{'}\) trouvée est inférieure à \(m\).

Nécessairement un ensemble de Noël dont la moyenne est minimale a pour plus grand élément 2512.

2) Peut-on avoir une moyenne minimale avec deux éléments \(x_i\) et \(x_{i+1}\) inférieurs à 2512 et non consécutifs ?

Si \(x_i < x_i+1 < x_{i+1}< 2512\), alors en remplaçant \(x_{i+1}\) par \(x_i+1\) dans l'ensemble, on obtient un nouvel ensemble de Noël et une nouvelle moyenne \[m^{'} = \frac{x_1 + x_2 + ... + x_n - x_{i+1} + x_i+1}{n}= \frac{m \times n- x_{i+1} + x_i+1}{n} = m + \frac{x_i+1- x_{i+1}}{n}.\] Vu que \(x_i+1- x_{i+1}\) est négatif, la nouvelle moyenne \(m^{'}\) trouvée est inférieure à \(m.\) Nécessairement un ensemble de Noël dont la moyenne est minimale est de la forme \(\{1; 2; ...;p; 2512\}.\)

3) La moyenne de cet ensemble de Noël est \[m=\frac{\frac{p(p+1)}{2}+2512}{p+1} = \frac{p}{2}+\frac{2512}{p+1}.\] On peut rechercher sur tableur la valeur de \(p\) comprise entre 1 et 2512 qui minimise \(\frac{p}{2}+\frac{2512}{p+1}\) ou bien étudier, en fonction de \(p\), le signe de \[\frac{p+1}{2}+\frac{2512}{p+2}-\frac{p}{2}-\frac{2512}{p+1}=\frac{1}{2}-\frac{2512}{(p+1)(p+2)}\] La moyenne de Noël est obtenue pour \(p = 70\) et elle est égale à \(\frac{4997}{71}.\)