Réponse : 2400

Voici la répartition des ampoules :

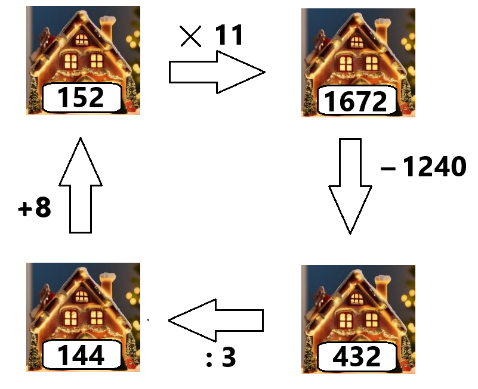
Explications :

Méthode 1 :

Voici à nouveau le schéma.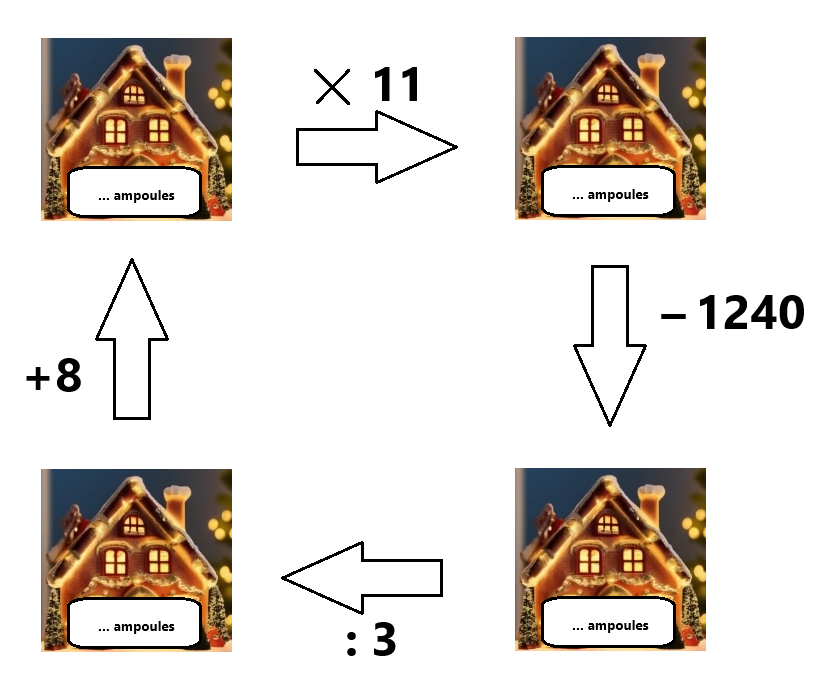

Si on nomme A et B le nombre d’ampoules dans les deux maisons de gauche sur le schéma de départ, on a donc :

• Un écart de 8 entre A et B, c’est-à-dire un écart de 24 entre 3A et 3B 
• Un écart de 1240 entre 11A et 3B.

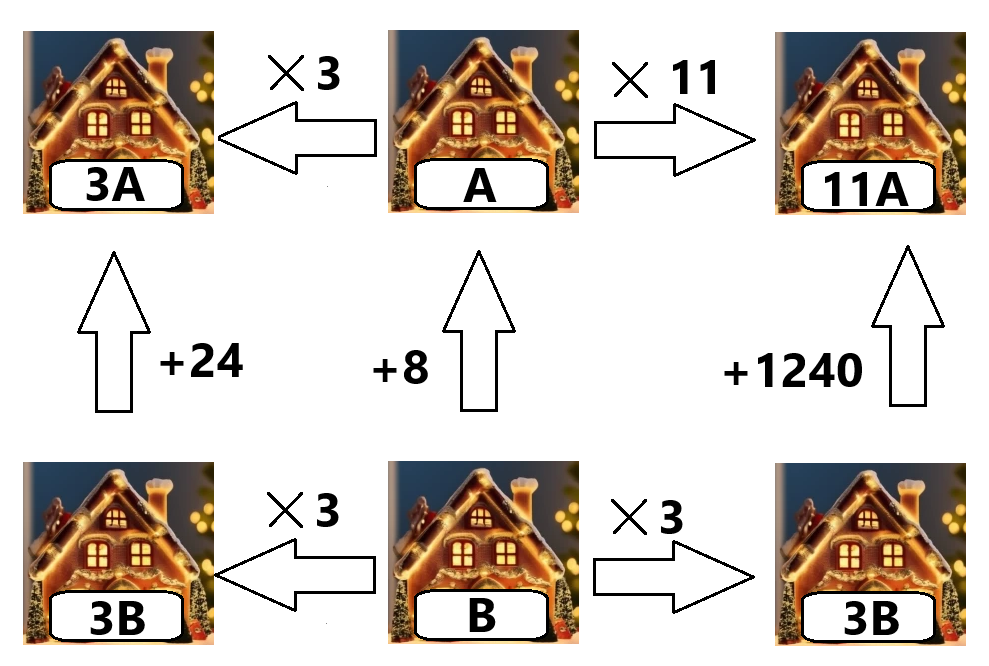
On peut donc dessiner un nouveau schéma avec les écarts entre 3B, 3A et 11A.

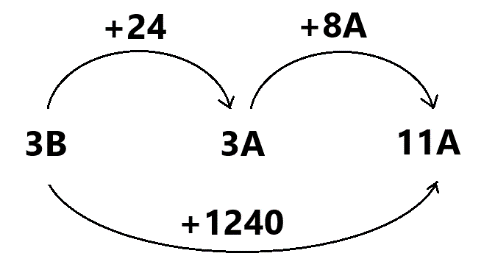
On en déduit que 8A = 1240 – 24, ce qui équivaut à A = 152.
Le schéma final est donc :

Le nombre total d’ampoules est donc : 152 + 1672 + 432 + 144 = 2400.

Méthode 2 :

Voici à nouveau le schéma.

On va créer une suite d'approximations successives de la solution, par une méthode itérative aussi appelée Méthode de point fixe. Les nombres d'ampoules sont entiers et clairement la maison en bas à gauche en a le moins. Si on part d'une valeur choisie au hasard du nombre d'ampoules de cette maison, on peut suivre les flèches, calculer les valeurs obtenues, et voir si on est revenu sur la bonne.
Essayons avec 0 ampoules : on trouve 8 pour la maison en haut à gauche, puis 88 pour celle en haut à droite. Puis un nombre négatif pour en bas à gauche, oups. Et quand on revient, on a aussi un nombre négatif d'ampoules : −384.
Essayons avec 100 ampoules : on trouve, dans l'ordre des flèches, 108 puis 1188, puis une valeur négative à nouveau : −52 puis une valeur non-entière −17,333…
Essayons avec 200 ampoules : on trouve, dans l'ordre des flèches, 208 puis 2288, puis 1048 puis une valeur non-entière −349,333…

On suspecte que la bonne valeur est entre 100 et 200 ampoules (dans la maison en bas à gauche). On constate aussi que la méthode est instable: elle tend à augmenter les écarts. Une bonne approche pour contrer cela est de prendre le système à l'envers. On va par moments diviser par 11 et tomber aussi sur des nombres non-entiers. On a plusieurs approches qui marchent, nous choisissons d'arrondir à l'entier le plus proche.

Partons de 100 ampoules en bas à gauche. On obtient 100×3 = 300 ampoules en bas à droite, puis 300+1240 = 1540 ampoules en haut à droite, puis 1540÷11 = 140 ampoules (coup de bol c'est un nombre entier) en haut à gauche et enfin 132 ampoules en bas à gauche.

Et on recommence : on obtient 132×3 = 396, 396+1240 = 1636, 1636÷11 = 148,72… arrondi à 149, 149−8 = 141. Bon, 141 ≠ 132 mais on voit que 132 est quand même une assez bonne valeur.

Donc on continue : 141×3 = 423, 423+1240=1633, 1663÷11 = 151,18… arrondi à 151, 151−8 = 143. On est tout proche !

Continuons : 143×3 = 429, 426+1240=1669, 1666÷11 = 151,72… arrondi à 152, 152−8 = 144.

Continuons : 144×3 = 432, 426+1240=1672, 1672÷11 = 152…, 152−8 = 144. C'est gagné : on a une solution du problème (mais dans cette méthode 2 nous n'avons pas démontré qu'elle est unique).

Quant au nombre total d'ampoules, c'est 144 + 432 + 1672 + 152 = 2400.

---

Énigme proposée par Fabrice Destruhaut