Niveau 1

Niveau 2

Réponse : 24

Explications :

Réponse : 11165

Explications :

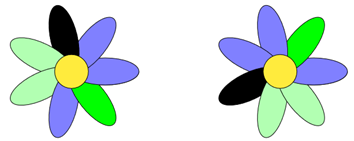
Si on ne demandait pas de compter les fleurs à rotations près, on raisonnerait simplement de la façon suivante : Il y a 7 pétales, chacun peut être d’une couleur parmi 5 possibles, il y a donc 5⁷ = 78125 fleurs possibles. Cependant, en faisant ça on compte certaines fleurs plusieurs fois. Plus précisément, à part les 5 fleurs complètement unies qu’on ne compte qu’une fois, on compte toutes les fleurs 7 fois. C’est une conséquence du fait que 7 est premier.

On peut le voir de différentes façons. Par exemple, pour une fleur donnée notons θ = k×2π/7 le plus petit angle tel que la fleur reste identique après rotation d’angle θ, avec k ∈ {1,…,7}.

Comme 7 est premier, si k ≠ 7 on peut trouver un entier n tel que nθ = 2π/7 modulo 2π, c’est à dire que k=1 est aussi un angle rendant la fleur invariante. Or si k = 1, tout pétale est de la même couleur que son voisin, donc la fleur est unie. En particulier, pour chaque fleur non-unie, k = 7. Par ailleurs, l’entier k est exactement le nombre de fois qu’on a compté une même fleur à rotation près.

Ainsi, le nombre de fleurs à rotation près est donc (5⁷-5)/7+5 = 11 165.

Explications détaillées:

Pour éviter de faire des dessins avec des couleurs, on va représenter chacune des 5 couleurs par des lettres A, B, C, D, E. Puis pour se détacher de la représentation géométrique de fleur à 7 pétales colorées, on va représenter la fleur par une séquence de 7 lettres prises chacune parmi les couleurs A, B, C, D, E. On a donc par exemple, les configurations suivantes :

• AAAAAAA
• AABBBBB
• ABCABCA

Il y a 5⁷ séquences différentes de lettres.

Cependant, nous en avons compté trop, puisqu’on nous demande de “compter les fleurs à rotation près”. Une rotation des pétales correspond à faire une permutation circulaire sur notre séquence de lettres. Ainsi (en faisant circuler les lettres vers la droite et en remettant la dernière en premier) :

Et on s’arrête car à l’étape d’après on retrouve la séquence initiale. On a donc ici 7 séquences différentes mais équivalentes que l’on a compté pour 7 au lieu de pour 1.

Donc toutes les séquences où l’on passe de l’une à l’autre par permutation circulaires sont équivalentes et forment un “paquet” que l’on ne devrait compter qu’une fois. Ces paquets forment bien une partition des 5⁷ combinaisons possibles : c’est à dire que chaque séquence est dans un seul paquet et que l’ensemble de tous les paquets couvre bien toutes les combinaisons possibles.

Mais quelles sont les tailles possibles de ces paquets ?

Remarquons que si l’on nomme k le nombre minimal de permutations circulaires (non nulles) qui redonne une séquence initiale, la taille du paquet est k. Bien sûr, dans le pire des cas, au bout de k=7 on retrouve la configuration initiale. On a vu sur l’exemple ci-dessus que l’on peut avoir k=7, mais peut-on avoir k<7 ?

Pour une séquence de la même couleur, par exemple AAAAAAA, la taille du paquet est k=1 et inversement si k=1 alors on a une séquence de même couleur. Il y a 5 séquences de ce type  : une par couleur et cela veut dire qu’on doit les compter chacune qu’une fois.

Peut-on avoir k = 2, 3, 4, 5, 6 ? En fait, en prenant quelques exemples, il semble que non et on devine que ç’est surement dû au fait que 7 est un nombre premier.

Conjecture : « Soit on a la même couleur et k=1, sinon k=7 ».

Si tel est le cas, on fait des paquets de 7 pour toutes les configurations qui ne sont pas de la même couleur et qui sont au nombre de 5⁷-5 séquences et donc le nombre de combinaisons possibles (à rotation près) est : (5⁷-5)/7+5 = 11165.

Mais est-ce que notre conjecture est vraie ? Saurait-on le démontrer ?

Pour que la configuration reste la même après une rotation de k pétales (où k=1,2,3,4,5 ou 6), les 7 pétales doivent être colorés de manière à former des groupes de répétition de taille divisant 7.

En effet, si l’on part d’une configuration initiale et qu’on retombe sur cette configuration initiale après k<7 rotations, c’est qu’il y a un bloc de k lettres qui se sont répétées.

Par exemple avec k=2 :

• Séquence initiale : abxxxxx (où ab peut être n'importe quelle couleur)
• Séquence au bout de k=2 : xxabxxx. Mais on a xxabxxx = abxxxxx car on retrouve la séquence initiale, si bien que cette séquence est ababxxx.
• Séquence au bout de k=4 := abababx (en répétant le processus)
• Séquence au bout de k=6 := bxababa (en répétant le processus). Et donc b=a (on a la même couleur, ce qui était exclu).
• A chaque étape on a le même motif ab qui se répète, mais on ne peut pas avoir n motifs ab (avec a différent de b) dans 7 car 2 ne divise pas 7.

On aura le même raisonnement avec k=3 à 6, puisque aussi k ne divise pas 7 qui est un nombre premier.

Donc on voit que comme 7 est un nombre premier, les seules répétitions possibles pour une configuration inchangée par une rotation (pour k de 1 à 6) sont celles où tous les pétales sont de la même couleur, c’est à dire k=1.

Pour aller plus loin :

Ce type de problème relève d'une branche des mathématiques appelée la combinatoire avec symétrie ou comptage de configurations sous symétries (où lorsque l'on parle de "symétrie" ici, on parle aussi des rotations). Le problème posé est un cas classique d’utilisation des outils de combinatoire pour compter les configurations de couleurs sous l'action des rotations. Ce type de problèmes est souvent résolu avec le théorème de Burnside (théorème vu en études supérieures). Pour le fait que si un motif se répète tous les k pétales, alors k serait un diviseur de 7, on pensera au théorème de Lagrange. Si tu aimes les problèmes de ce genre, la vidéo suivante (de niveau universitaire) devrait t’intéresser : Action de groupe (6/6), Formule de Burnside et applications, Gilles Bailly-Maitre.