Solution du défi
Choisis l'énigme dont tu veux voir une solution.
Remerciements :
Deeplawmath (ou Sébastien Kernivinen) remercie les personnes de son
entourage, notamment Hervé Lebris (Pleumeur-Bodou) pour leurs échanges
qui furent le point de départ de la création de cette énigme.
Première explication :
Regardons d’abord juste le cas de l’Auvergnat âgé de Apr (présent) ans et du Breton âgé de Bpr ans.
La phrase implique que Apr > Bpr. L'écart d entre l'âge des 2 personnes est constant : quel que soit leur âge, ils auront toujours d = (Apr - Bpr ) années d’écart.
Plaçons ces âges sur l’axe des entiers :
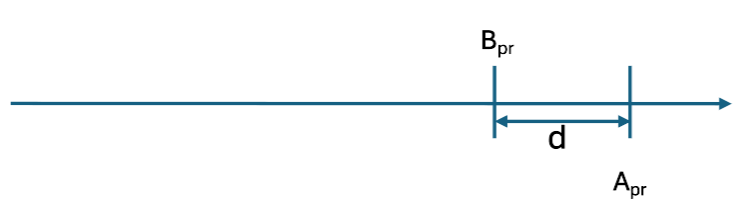
« Quand j’avais l’âge Apa que vous avez »: on avait donc un âge Apa (passé) qui est égal à Bpr , c’est à dire Apa = Bpr , que l’on visualise :

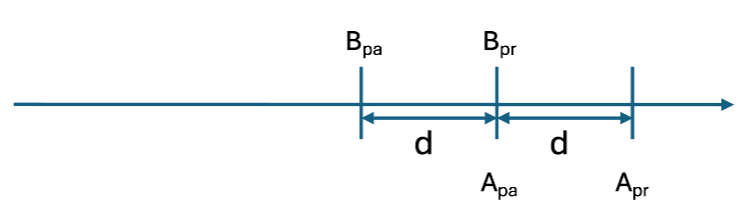
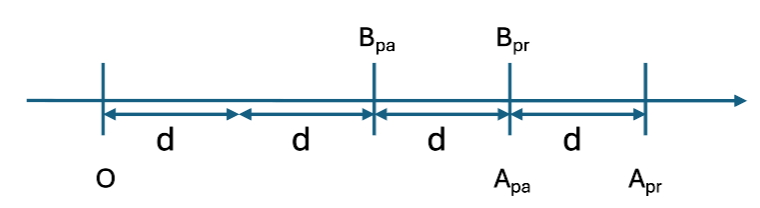
En répétant le raisonnement avec les autres « couples » de personnes on obtient :
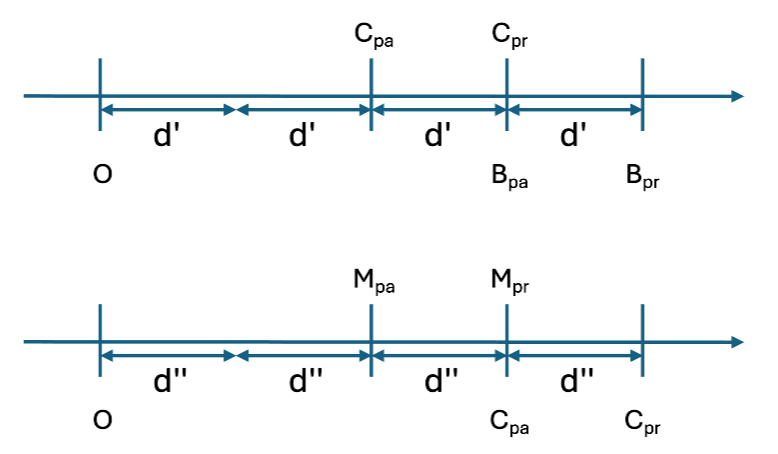
Apr=4d, Bpr=3d=4d’, Cpr=3d’=4d’’ et Mpr=3d’’.
En mettant la même variable partout :
Apr=4d, Bpr=3d, Cpr=(9/4)d et Mpr=(27/16)d.
Les personnages ont au moins de 125 ans donc Apr=4d < 125, c’est à dire d<31.
Or d et les âges sont entiers et l'on a Mpr = (27/16) d, si bien que d est un multiple de 16 inférieur à 31, c’est à dire d=16.
En conclusion :
Apr=4×16=64, Bpr=3×16=48, Cpr=(9/4)×16=36 et Mpr=(27/16)×16=27.
La solution est donc (Apr, Bpr, Cpr, Mpr) = (64,48,36,27).
On saisit 64,48,36,27.
Deuxième explication :
Notons a, b, c, m respectivement les âges actuels de l’Auvergnat, du Breton, du Corse et du Mahorais.
Regardons d’abord juste le cas de l’Auvergnat et du Breton.
Il est à noter que leur écart d'âge d = a-b est un invariant. On peut représenter la situation dans le tableau suivant :

* quand j'avais l'âge que vous avez
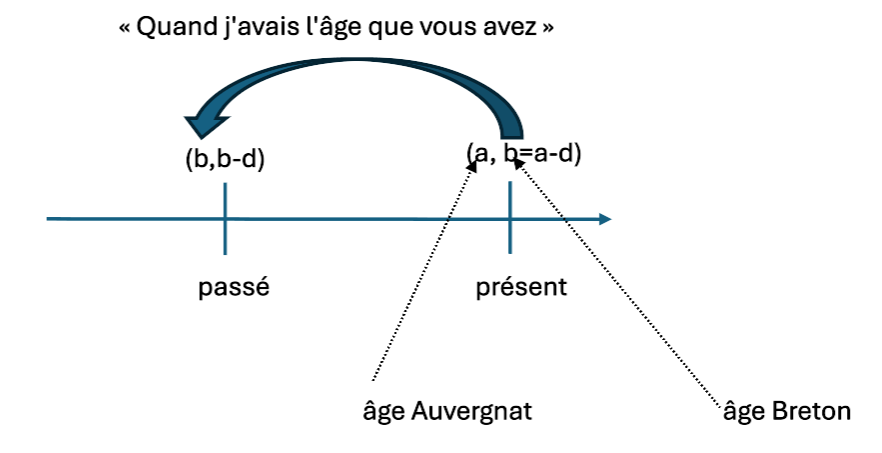
« Mon âge a est aujourd’hui le double de l’âge que vous aviez 2b-a quand j’avais l’âge b que vous avez aujourd’hui »donne donc simplement la relation : a = 2 (2b-a), c’est à dire a = (4/3) b. On voit donc comment l’âge du « premier » se déduit de l’âge du « deuxième ».
Il vient alors :
b = 4/3 c
c = 4/3 m
b = (4/3)^2 m
c = (4/3) m
Comme a, b, c et m sont des nombres entiers, la première relation nous donne que m doit être un multiple de 3^3=27. Avec m=27, il vient a=4^3 = 64, b = 48, c = 36. Les autres multiples de 27 ne conviennent pas car avec le plus petit qui est alors m=27×2, on aurait a = 64×2 = 128 > 125.
La solution est donc (a,b,c,m) = (64,48,36,27).
On saisit 64,48,36,27.
Remerciements :
Deeplawmath (ou Sébastien Kernivinen) remercie les personnes de son
entourage, notamment Hervé Lebris (Pleumeur-Bodou) pour leurs échanges
qui furent le point de départ de la création de cette énigme.
Première explication :
Appelons A l’âge (en années) du premier. Comme le premier dit au
deuxième « quand j’avais l’âge que vous avez », il est plus
vieux que le deuxième. Appelons d la différence d’âge entre le deuxième
et le premier.
« J’avais l’âge que vous avez » il y a d années. Il y a d
années, votre âge était A – d et mon age actuel est
A + d. Donc A + d = 2 (A – d),
c’est-à-dire A = 3d.
Le premier et le second ont donc des âges de la forme 4d et 3d.
Réciproquement, si deux personnes ont des âges de la forme 3d et 4d
alors l’âge 4d du second est bien le double de 2d, soit 3d – d,
autrement dit, l’âge du premier il y a d années, c’est-à-dire
« quand le second avait l’âge du premier ».
La déclaration de celui qui parle implique que l’âge A du premier est un
multiple de 3 et l’âge A + d du second est un multiple de 4 ;
précisément, on a successivement :
A = 3d (le premier parle au deuxième)
A + d = 4d = 3d’ (le deuxième est interpellé par le premier et il parle au troisième)
A + d + d’ = 4d’ = (16/3)d = 3d’’ (on passe de l’âge de l’un au suivant en multipliant par 4/3)
A + d + d’ + d’’ = 4d’’ = (64/9)d
En résumé, les âges (entiers naturels) des personnes du groupe sont de la forme ( 3d , 4d , (16/3)d , (64/9)d ).
Donc d est un multiple de 9.
Seule la valeur d = 9 est envisageable (car « moins de 125
ans ») et conduit à la solution : 27, 36, 48, 64 qui sont les
âges, en années, des quatre personnes.
Le groupe d’amis est constituée de quatre membres au maximum car l’âge
d’une 5ème personne dépasserait 128 (d = 18, a minima).
Deuxième explication :
1. De combien de personnes est formé le groupe au maximum ?
Notons a1, a2, .., an respectivement
les âges du n-ième élément, du n-ième -1, ... du deuxième et du premier du
groupe. Ici on a inversé l’ordre pour avoir les âges dans un ordre
croissant.
Il est à noter que l’écart d'âge est un invariant.
On peut représenter la situation dans le tableau suivant :
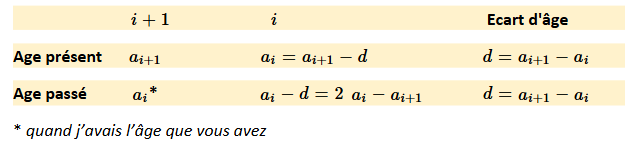
« Cette année est exceptionnelle car mon âge ai+1 est le double de l’âge que vous aviez 2 ai - ai+1 quand j’avais l’âge ai que vous avez aujourd’hui »donne simplement : ai+1 = 2 ai - ai+1 et donc ai+1 = (4/3) ai.
C’est donc une suite géométrique de raison (4/3) et de premier terme a1. On a donc l’expression explicite ai = (4/3)^(i-1) a1.
On peut avoir n=2, n=3, n=4 mais pas n>4.
En effet, comme les ai sont des nombres entiers, la relation an = (4/3)^(n-1) a1 nous donne que a1 doit être un multiple de 3^(n-1) et l’on a alors au minimum an = 4^(n-1), ce qui donne 64 pour n=4 et 256 > 125 pour n=5.
Le groupe est donc formé au maximum de n = 4 personnes.
2. Quels sont les âges des personnes du groupe de 4 personnes ?
Avec a1 =27, il vient a4 =4^3 = 64, a3 = 48, a2 = 36. Les autres multiples de 27 ne conviennent pas car avec le plus petit qui est alors a1 =27×2, on aurait a4= 64×2 = 128 > 125.
La solution est donc (a4,a3,a2,a1) = (64,48,36,27).
Question bonus :
On dit qu’un membre du groupe est le « Passettefoa » d’un autre membre lorsque la somme de leurs âges n’est pas un multiple de sept. Est-il VRAI ou FAUX de dire : « Dans le groupe de personnes, chaque membre possède un unique Passettefoa et ce n’est pas la personne à laquelle il a parlé » ?
Réponse : C'est VRAI.
Explication 1 :
Les sommes de deux âges consécutifs sont de la forme 3a + 4a = 7a i.e. des multiple de sept. De plus, la somme 27 + 64 = 13×7 est un multiple de sept alors que les sommes 27 + 48 = 75 et 36 + 64 = 100 ne sont pas des multiples de sept.
Explication 2 :
On peut remarquer que le terme de la suite géométrique s’écrit aussi (en prenant a1 =3^3),
ai = 4^(i-1)×3^(4-i).
La sommes de deux âges consécutifs est donc de la forme
ai+1+ ai = 4^(i)×3 ^(4-i-1) + 4^(i-1)×3^(4-i)
= 4 ^(i-1)×3^(4-i-1) [4 + 3]
= 4 ^(i-1)×3^(4-i-1) 7
qui est un multiple de 7.
De plus, la somme 27 + 64 = 13×7 est un multiple de sept alors que les sommes 27 + 48 = 75 et 36 + 64 = 100 ne sont pas des multiples de sept.
On peut résumer cela sur le graphe suivant :
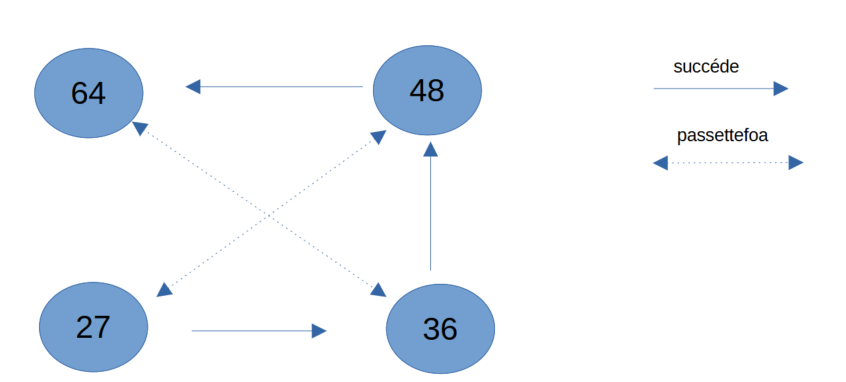
Retour au calendrier.