Observons l’ordre du jeu avant et après la donne australienne, en nous concentrant dans un premier temps sur l’impact du déplacement de la première carte :

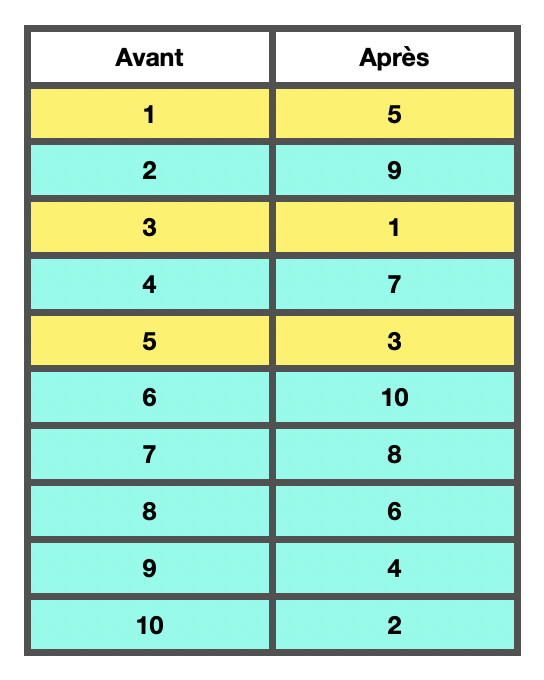
• La carte en première position est passée en 3ème position.
• Pendant ce temps, la carte en 3ème position est passée en 5ème position.
• La carte en 5ème position, quant à elle, est passée en première position.

Cela nous permet de repérer ce que l'on appelle joliement une orbite circulaire, c'est à dire un ensemble de cartes qui vont s'échanger ainsi :

Au bout de 3 donnes australiennes, la première, la troisième et la cinquième carte reviennent donc à leurs positions initiales ! N’hésitez pas à essayer !

Cependant, tout le paquet n’est pas revenu dans sa position initiale. Pour le comprendre, il nous faut observer l’orbite de la 2ème carte ! La voici :

La 2ème carte, comme toutes les cartes de son orbite, attendra donc 7 donnes australiennes avant de revenir pour la première fois à sa position de départ.

Remarquons enfin que ces deux orbites contiennent à elles deux les 10 cartes du jeu. Il n’y a donc pas d’autres orbites à étudier.

Finalement, notons N le nombre de donnes australiennes effectuées sur notre paquet de 10 cartes. Pour que le jeu soit dans sa position initiale, il faut simultanément :

• Que N soit un multiple de 3 (pour que les cartes 1, 3 et 5 soient à leur place)
• Que N soit un multiple de 7 (pour que les cartes 2, 4, 6, 7, 8, 9 et 10 soient à leur place)

Le nombre minimal de donnes australiennes à effectuer avant que le jeu ne revienne dans sa position initiale est donc le plus petit commun multiple à 3 et 7, c’est-à-dire 21, vu que 3 et 7 sont premiers entre eux.

Reprendre l’énigme pour un paquet de 17 cartes, puis de 52 cartes, puis vérifier vos résultats informatiquement, par exemple à l’aide d’un programme en python !

Énigme proposée par Marc Weber