Il existe quatre quartiers de Noël différents qui ont des bords Ouest et Nord ordonnés (10, 20, 30, 40). (En raisonnant de façon exhaustive sur une des maisons non colorées).

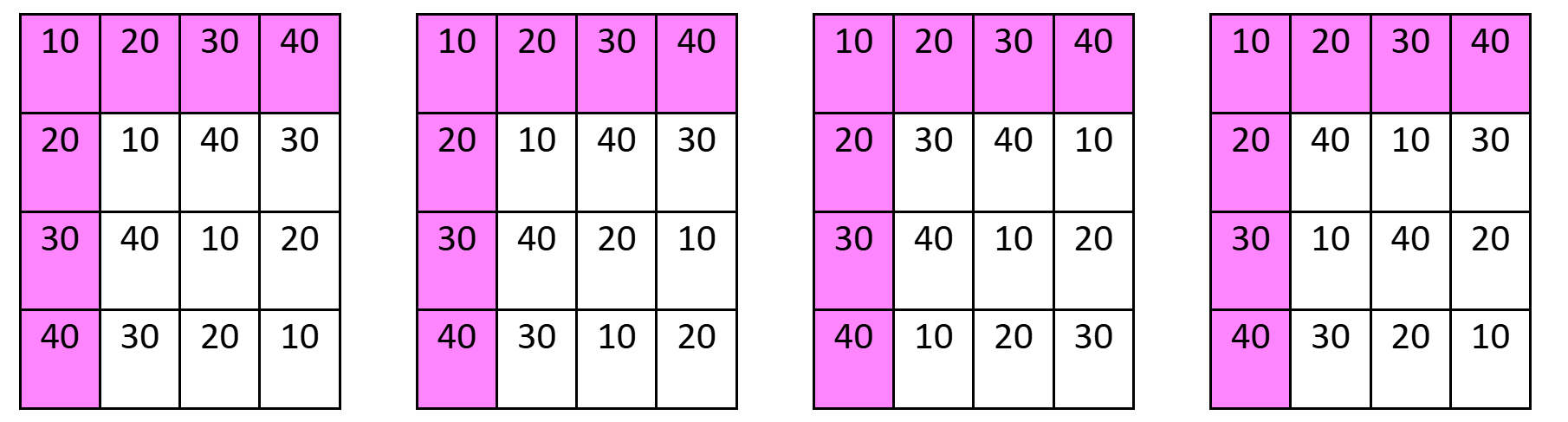
Tout quartier de Noël peut être ramené à l'un des quatre quartiers de Noël ci-dessus et à un seul car la seule composition de permutations sur les colonnes puis sur les lignes qui permet de le faire est entièrement déterminée par les bords Ouest et Nord initiaux. L'ensemble des quartiers de Noël est donc constitué de quatre classes disjointes, dont chacune contient exactement un des quatre quartiers de Noël « ordonnés » ci-dessus.

De plus, il y a autant de quartiers de Noël dans chaque classe que de permutations de colonnes fois le nombre de permutations de lignes conservant la première ligne.

Le nombre de plans de quartiers de Noël est donc donné par le produit :  

Il est intéressant de connaître alors les définitions de carrés latins et de carrés gréco latins, qui nous amènent par exemple à la construction de carrés magiques.