Solution du défi
Autrement dit, il faut mettre la masse de 700 kg sur l'attache numéro 8 et celle de 500 kg sur la numéro 2.
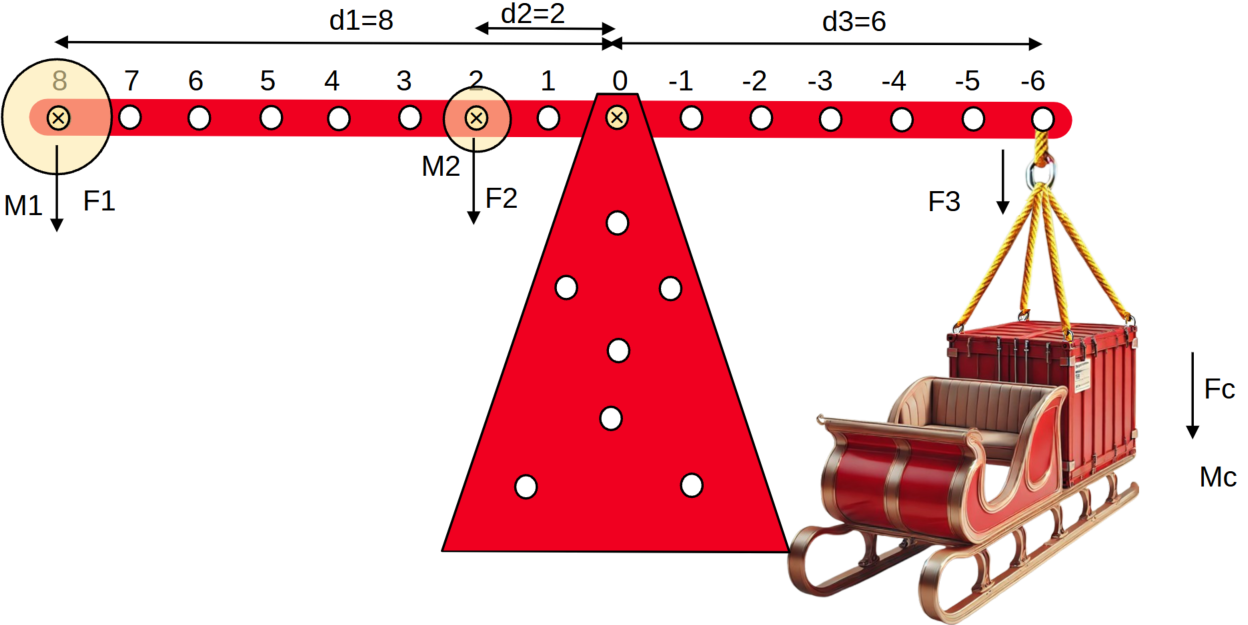
Explications :
1. Condition d'équilibre
Comme indiqué, on a la relation suivante pour un équilibre parfait :
En remplaçant les valeurs, on obtient :
700×d1 + 500×d2 − 6×1100 = 0.
Soit :
700×d1 + 500×d2 = 6600.
2. Equation à résoudre
Cela donne l'équation simplifiée :
7×d1 + 5×d2 = 66.
Les positions d1 et d2 doivent respecter les limites données par l'énoncé : d1 (respectivement d2) est un entier relatif dans l'intervalle [−6,+8]. (Un éventuel zéro signifierait qu'on doit placer le poids sur l'axe. Or il n'a pas d'attache à cet endroit. Qu'à cela ne tienne : un poids sur l'axe ne sert à rien. Donc un 0 signifie : ne pas mettre de poids.)
3. Résolution 1
On cherche toutes les solutions à cette équation.
Nous réarrangeons l'équation pour obtenir d2 :
d2 = (66 − 7×d1) / 5.
Il nous suffit de tester les valeurs possibles de d1 dans l'intervalle [−6,+8] et de vérifier si d2 est un entier appartenant à cet intervalle.
| d1 | d2 calculé | Solution valide ? |
|---|---|---|
| 8 | 2 | Oui |
| 7 | 3.4 | Non |
| 6 | 4.8 | Non |
| 5 | 6.2 | Non |
| 4 | 7.6 | Non |
| 3 | 9 | Non |
Pour équilibrer une masse de 1100 kg située à droite en −6 à l'aide de deux masses, dont l'une est de 700 kg et l'autre de 500 kg (soit un total de 1200 kg), nous avons d'abord pensé à placer la masse de 700 kg plutôt à gauche, vers la position 6. Cette configuration n'a pas fonctionné, alors nous avons testé les positions environnantes, notamment 7, 8, 5 , 4 et 3.
La position 3 permet bien d'obtenir une valeur entière pour la position d2, mais celle-ci vaut 9, alors que la dernière attache porte le numéro 8. Nous n'avons pas testé les valeurs plus petites de d1, car nous savions que cela rendrait d2 encore plus grand.
4. Résolution 2
On doit résoudre dans les entiers relatifs l’équation :
7×d1 + 5×d2 = 66
Les multiples de 5 terminent par 0 ou 5.
- Si c’est 0, alors 7×d1 a 6 comme unité s'il est positif, et 4 s'il est négatif donc comme d1 est compris entre –6 et 8, ça ne peut être que d1=8 ou d1=–2. Et alors on a d2=2 dans le premier cas et d2=16 dans le second, ce qui est exclu. Pour finir, (d1,d2) = (8,2) est bien une solution valide. Est-ce la seule ?
- Si c’est 5, alors 7×d1 = 66 − 5×d2 se termine par 1 s'il est positif ou un 9 s'il est négatif, et donc comme d1 est compris entre –6 et 8, ça ne peut être que d1=3. Et on a alors d2=9, ce qui est exclu également.
5. Conclusion
La seule solution valide est d1=8 et d2=2 : la masse de 700 kg sur l'attache numéro 8 et celle de 500 kg sur la numéro 2.
Dis-toi que tes cadeaux sont dans un de ces conteneurs et vont bientôt arriver chez toi grace à ce dispositif étonnant et bien calculé.
Remerciements :
Merci au site http://cm1cm2.ceyreste.free.fr/leviers.html, qui a été une source d’inspiration. On y trouvera une présentation assez simple des équilibres, expliqués de façon très imagée pour les plus jeunes.
Retour au calendrier.