Une recherche sur Internet, ou le 1er indice, nous apprend qu'une grossesse est dite (en France) à terme si la naissance a lieu entre la 37e et la 40e semaine.* Il s'est donc déroulé au moins 7 × 37 = 259 jours depuis le début de la grossesse.

*: plus précisément on compte les semaines de grossesse à partir de l'aménorrhée.

La première échographie doit se faire entre 11 semaines + 3 jours et 13 semaines + 6 jours, soit entre 80 et 97 jours. Ainsi la date de naissance et celle de l'échographie diffèrent d'au moins 259 − 97 = 162 jours.

Au jour J1 de ses 6 mois, Joséphine a au moins 31 + 28 + 31 + 30 + 31 + 30 = 181 jours. Cela fait donc au moins 162 + 181 = 343 jours depuis l'échographie en question.

Le premier prix Abel a été décerné en avril 2003 et la première femme a l'avoir reçu est Karen Uhlenbeck, en mars 2019. Comme au jour J1 Emmie se demande quand on attribuera ce prix à une femme, c'est qu'il se situe entre ces deux dates.

Nous allons voir à quel point on peut situer J1 avec ces deux informations, que nous résumons ci-dessous.

• J1 est situé dans la période entre avril 2003 et mars 2019.
• Il n'y a pas de vendredi 13 dans la période de 343 jours consécutifs finissant au jour J1.

On se procure un tableau des vendredi 13 couvrant la période concernée, plus le 1er vendredi 13 avant cette période, ou on les repère à la main sur un calendrier. On peut aussi demander directement à une IA (attention toutefois à l'empreinte carbone). Ou encore écrire soi-même un petit script informatique, c'est un exercice intéressant. Par exemple en Python3, avec la bibliothèque datetime :

from datetime import date

for annee in range(2002,2019+1): # de 2002 inclus à 2020 exclu

  # en 2019, s'arrêter en mars
  mois_max = 12 if annee < 2019 else 3

  for mois in range(1,mois_max+1): # de 1 inclus à mois_max+1 exclu

    objet = date(annee,mois,13) # création d'un objet de type date

    if objet.weekday() == 4: # teste si c'est bien un vendredi

      # alors écrit la date
      print(objet.strftime("%d/%m/%Y")) 

13/12/2002, 13/06/2003, 13/02/2004, 13/08/2004, 13/05/2005, 13/01/2006, 13/10/2006, 13/04/2007, 13/07/2007, 13/06/2008, 13/02/2009, 13/03/2009, 13/11/2009, 13/08/2010, 13/05/2011, 13/01/2012, 13/04/2012, 13/07/2012, 13/09/2013, 13/12/2013, 13/06/2014, 13/02/2015, 13/03/2015, 13/11/2015, 13/05/2016, 13/01/2017, 13/10/2017, 13/04/2018, 13/07/2018.

Les nombres de jours d'écarts entre deux vendredis 13 consécutifs dans cette liste sont les suivants (on peut aussi calculer les écarts de dates en Python3) :

du 13/12/2002 au 13/06/2003 : 182 jours
du 13/06/2003 au 13/02/2004 : 245 jours
du 13/02/2004 au 13/08/2004 : 182 jours
du 13/08/2004 au 13/05/2005 : 273 jours
du 13/05/2005 au 13/01/2006 : 245 jours
du 13/01/2006 au 13/10/2006 : 273 jours
du 13/10/2006 au 13/04/2007 : 182 jours
du 13/04/2007 au 13/07/2007 : 91 jours
du 13/07/2007 au 13/06/2008 : 336 jours
du 13/06/2008 au 13/02/2009 : 245 jours
du 13/02/2009 au 13/03/2009 : 28 jours
du 13/03/2009 au 13/11/2009 : 245 jours
du 13/11/2009 au 13/08/2010 : 273 jours
du 13/08/2010 au 13/05/2011 : 273 jours
du 13/05/2011 au 13/01/2012 : 245 jours
du 13/01/2012 au 13/04/2012 : 91 jours
du 13/04/2012 au 13/07/2012 : 91 jours
du 13/07/2012 au 13/09/2013 : 427 jours
du 13/09/2013 au 13/12/2013 : 91 jours
du 13/12/2013 au 13/06/2014 : 182 jours
du 13/06/2014 au 13/02/2015 : 245 jours
du 13/02/2015 au 13/03/2015 : 28 jours
du 13/03/2015 au 13/11/2015 : 245 jours
du 13/11/2015 au 13/05/2016 : 182 jours
du 13/05/2016 au 13/01/2017 : 245 jours
du 13/01/2017 au 13/10/2017 : 273 jours
du 13/10/2017 au 13/04/2018 : 182 jours
du 13/04/2018 au 13/07/2018 : 91 jours

On va explorer la position de tous les vendredi 13 sur un siècle de notre calendrier (le calendrier grégorien).

On va travailler modulo 7 et on numérote les jours de 0 à 6 : 0 pour dimanche, 1 pour lundi, 2 pour mardi, 3 pour mercredi, 4 pour jeudi, 5 pour vendredi et 6 pour samedi. D'un mois M au suivant M+1 le numéro n associé au 13^e jour du mois change à (n + d) modulo 7, où d = 28, 29, 30 ou 31 est le nombre de jours du mois M. Notons que 31 = 4×7 + 3, donc si d = 31 alors (n + d) = (n + 3) modulo 7.

Pour éviter des phrases à rallonge, on va donner un nom au numéro J entre 0 et 6 associé au jour (dimanche, lundi, etc) de la semaine où tombe le 13 jour d'un mois M donné : on dit que J est le code de M. Ainsi on cherche tous les mois M dont le code vaut 5 (5=vendredi).

Ci-après, nous avons répertorié le nombre de jours de mois sur une durée d’un an en commençant par le mois de mars ainsi qu'en vert le décalage du code du mois par rapport au suivant. En procédant ainsi, le dernier jour de l’année-décalée (une décannée) est le 28 ou le 29 février et une décannée comporte 365 ou 366 jours. L’avantage est qu’en considérant une décannée, les décalages cumulés d’un jour de semaine d’un mois à un autre sont toujours les mêmes, que l’année soit bissextile ou non. Le décalage entre le dernier mois de la décannée A et le premier mois de la décannée A+1 dépend du caractère bissextile de l'année A.

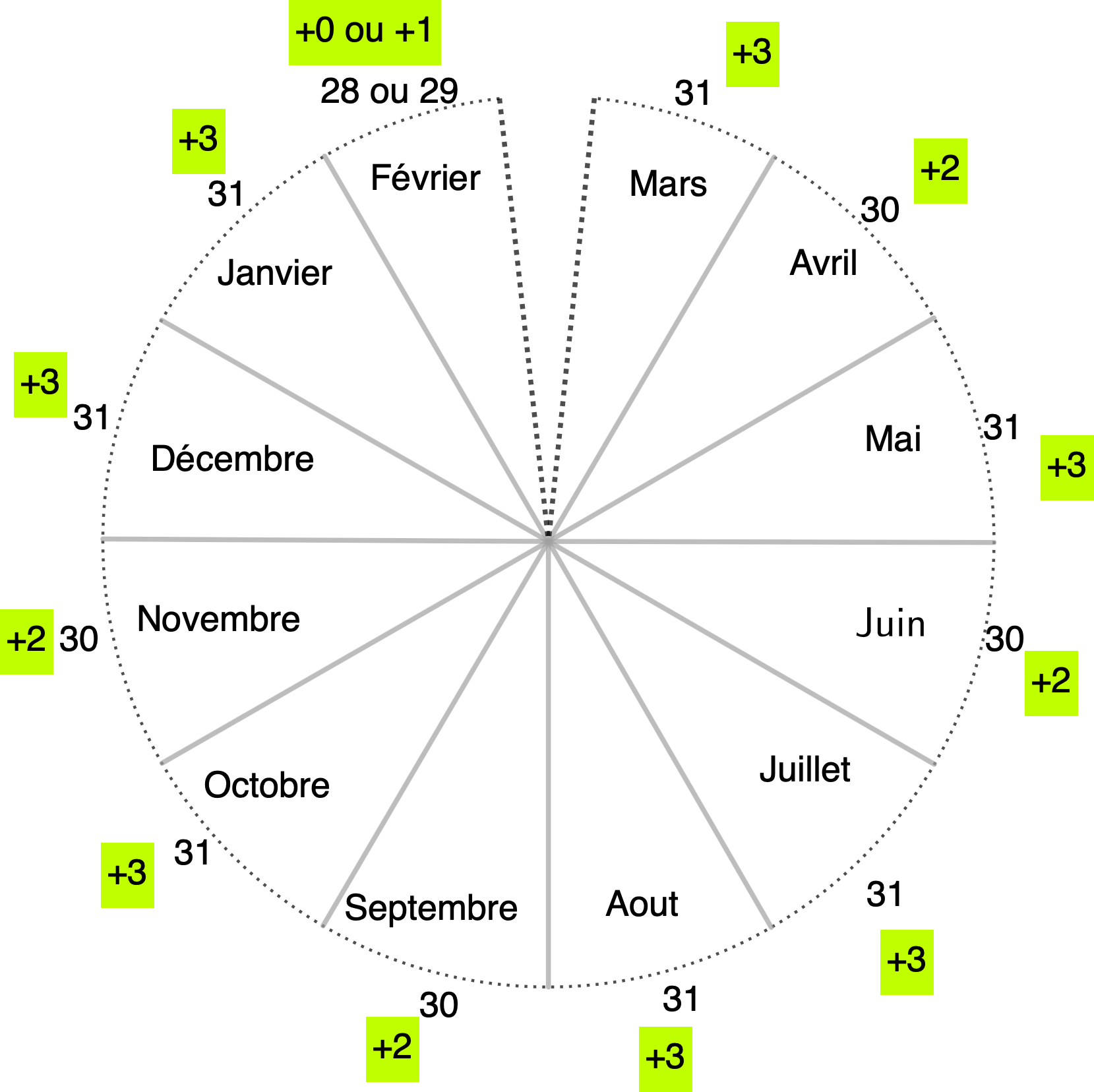
En cumulant ces décalages, on obtient les codes des mois d'une décannée en fonction des code J de son premier mois (le mois de mars, donc).

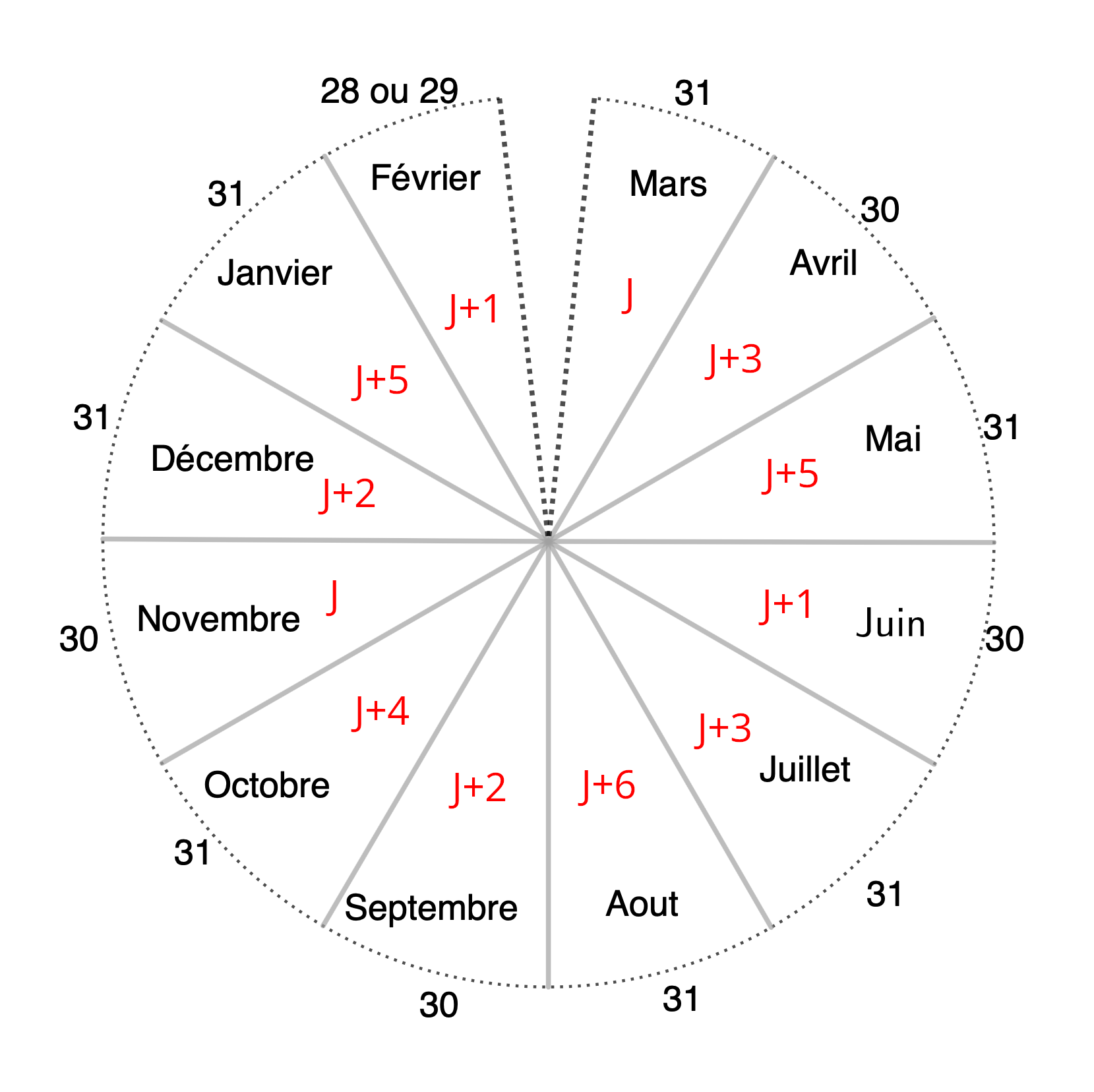
Déjà on voit que toute décannée contient au moins un vendredi 13 (et au plus deux).

Les mois avec un 11 rouge correspondent à un écart de 335 jours à la fois pour le mois de juillet ou octobre d'une décannée bissextile (donc l'année précédant une année bissextile). Ce n'est pas assez pour contenir un intervalle de 343 jours consécutifs. Donc seuls les deux cas avec un 14 rouge peuvent contenir un tel intervalle : du 13 juillet d'une année précédant une année non-bissextile au 13 septembre de l'année suivante, ou du 13 août d'une année précédant une année bissextile au 13 octobre de l'année suivante.

Il ne nous reste plus qu’à chercher, en quelles années, entre 2002 et 2019, le 13 juillet est tombé un vendredi sans que l’année suivante ne soit bissextile et en quelles années précédant une année bissextile le 13 août est tombé un vendredi. À l’aide de l’agenda ou bien de l’algorithme de Conway (et de quelques essais), d'un programme ou autre, on obtient une seule possibilité : la période entre le 13 juillet 2012 et le 13 septembre 2013. On conclut alors comme dans la méthode 1.