Réponse : 4

Explications :

Chaque personne a serré la main d’un nombre compris entre 0 et 8 de personnes. Ainsi, exactement une personne parmi Mme Noël et les invités (c'est à dire autre que M. Noël) a serré respectivement la main de 0, 1, 2, …, 8 personnes au cours de la soirée. Pour M. Noël, on n'a pas encore d'information.

Regardons les personnes autres que M. Noël. La personne ayant serré la main de 8 personnes ne peut être couple qu’en avec celle qui en a serré 0, car c’est la seule personne qu’elle n’a pas saluée, donc toutes les autres ont serré une main.

Sachant cela, un raisonnement analogue montre que la personne ayant serré la main de 7 personnes est en couple avec celle en ayant serré la main d'une seule personne. Puis celle ayant serré 6 est avec celle ayant serré 2, et celle ayant serré 5 avec celle en ayant serré 3.

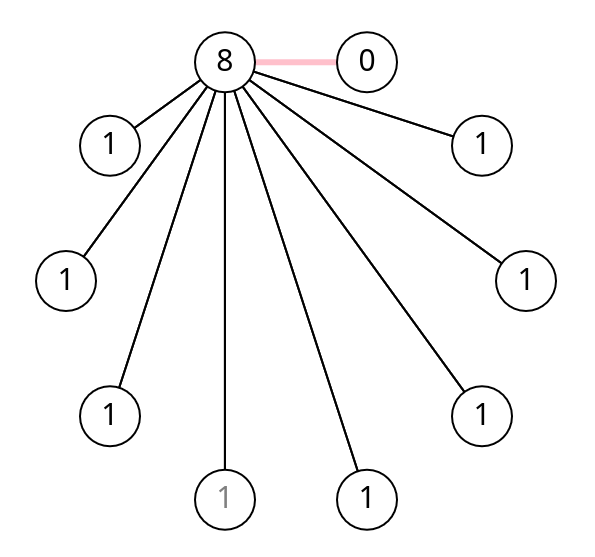
Il reste alors deux personnes, dont M. Noël et une personne qui a serré la main de 4 personnes. Elles sont en couple car on a vu que les 4 autres sont en couples entre elles (8 avec 0, 7 avec 1, 6 avec 3 et 5 avec 2). L'autre personne est donc Mme Noël.

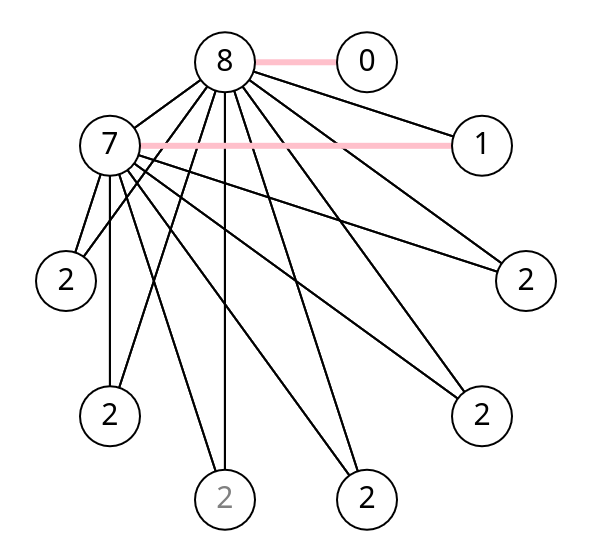
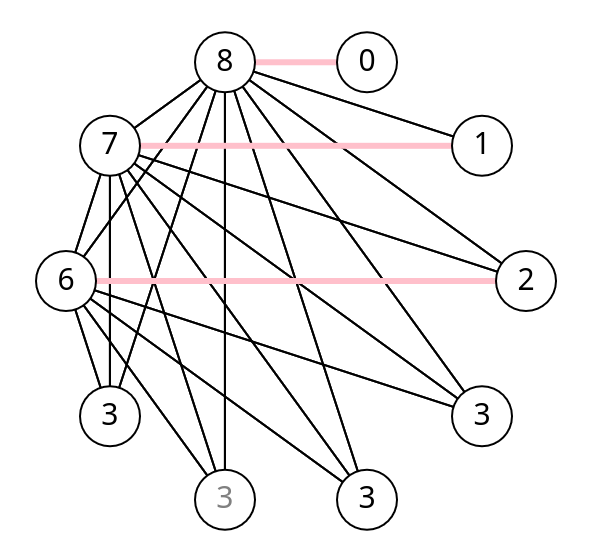
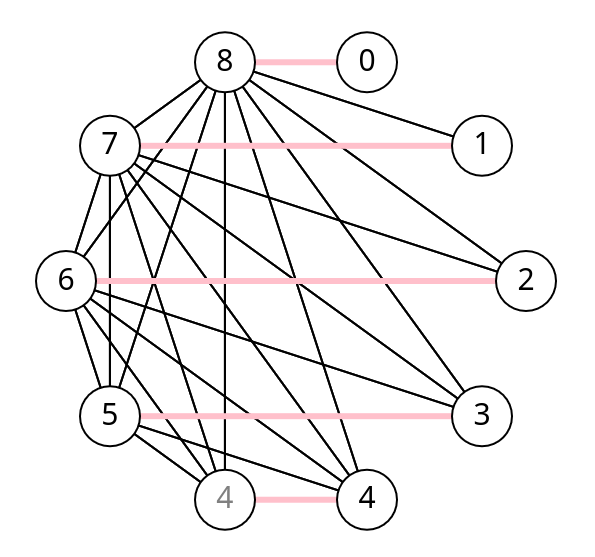
Bonus : M. Nöel a également serré la main de 4 personnes. En effet il n'a pas serré la main de sa femme et l'analyse ci-dessus montre en fait que 8,7,6 et 5 lui ont serré la main mais pas 0,1,2 ni 3.

Seconde Explication :

Nous proposons une approche par récurrence.

Note : pour simplifier la rédaction on va supposer que deux personnes qui se sont serré la main ne l'ont fait qu'une fois et n'ont serré qu'une main de l'autre personne. Bien sûr cela ne change rien au résultat.

Énoncé pour \(n\) couples

On a \(n\) couples, soit \(2n\) personnes. Une personne (que nous nommerons l'observateur) constate que les \(2n-1\) autres personnes ont chacune serré un nombre différent de mains. Quelle sont les valeurs \(m_n\) et \(m'_n\) du nombre de mains qu’a serrées cette personne et son conjoint ?

Solution

Premiers éléments

Une personne peut au maximum avoir serré la main de toutes les personnes hors son(-sa) propre partenaire. Elle a donc au plus \(2n-2\) poignées de main possibles. Ainsi, les \(2n-1\) valeurs différentes observées parmi les autres personnes sont nécessairement : \[ 0, 1, \ldots, 2n-2. \] De plus, celui qui n’a serré aucune main (valeur \(0\)) doit être le partenaire de celui qui a serré toutes les mains sauf celle de son partenaire (valeur \(2n-2\)). En effet, sinon la personne de valeur \(0\) lui aurait serré la main. On sait donc qu’il existe un couple ayant les valeurs de poignées (\(0, 2n-2\)) et qui ne contient pas l'observateur. On va faire une récurrence sur le nombre de couples. On va noter \(O\) l'observateur et \(A_0\), \(A_1\), \(\ldots\), \(A_{2n-1}\) les autres, indexées en fonction du nombre de mains serrées.

Initialisation (cas \(n = 2\))

Avec \(2\) couples, on a vu ci-dessus que l'un des couples est \((A_0,A_2)\). Le couple restant est \((O,A_1)\), donc \[ m'_2 = 1. \] Notons que \(A_2\) n'ayant pas serré la main de son conjoint \(A_0\), il a serré les mains de \(O\) et \(A_1\). Quand à \(O\), il n'a pas pu serrer la main de son conjoint \(A_1\), ni de \(A_0\). Ainsi \[ m_2 = 1. \]

Hérédité

Supposons que la valeur de \(m_n\) et \(m'_n\) sont connues pour le problème à \(n\) couples. On considère le problème à \(n+1\) couples, soit \(2n+2\) personnes. Par l'analyse préliminaire (voir la section premiers éléments ci-dessus) on sait qu'un des couples est \((A_0,A_{2n})\) (le nombre maximal de poignées de mains est ici \(2(n+1)-2 = 2n\)). Retirons ce couple du décompte : il n'y a plus que \(n\) couples et nous devons retirer les poignées de mains données par ce couple, c'est à dire par \(A_{2n}\) puisque \(A_0\) n'en a pas donné. Les poignées de mains restantes se sont données entre les couples restants et chacun a un décompte qui est diminué de \(1\) : \(A_1\) en a donné \(0\), \(A_2\) en a donné \(1\), etc. On se retrouve alors dans la situation du problème à \(n\) couples. On en déduit que \[ m_{n+1} = m_{n}-1 \text{ et } m'_{n+1} = m'_{n}-1 \] Comme \(m_2 = m'_2 = 1\), on en déduit par récurrence : \[ m_n = m'_n = n - 1. \]

Exemple

Pour \(n = 5\) couples (soit \(10\) personnes), on a donc : \[ m_5 = m'_5 = 5 - 1 = 4. \]

Références : on pourra consulter cette vidéo sur YouTube ou l'article suivant sur le site Culture Mathématiques.