On remarquer d'abord que les zones d’une couleur donnée ne partagent un bout de courbe qu’avec des zones de deux autres couleurs différentes. Par exemple, pour le rose c’est le turquoise et le violet. Et pour le turquoise, c’est le rose et l’orange. Du coup, la zone A est forcément orange ou rose et la zone B violette ou turquoise.

L'astuce pour décider lesquelles de ces possibilités est la bonne consistait à :

• Considérer les lignes blanches comme une seule et même courbe où, à chaque croisement, on va tout droit.
• Parcourir cette courbe dans un sens et tenir compte de ce sens de parcours (on parle d'orientation) dans l'analyse.
Pour le second point, on peut dessiner des petites flèches comme sur l'image suivante.

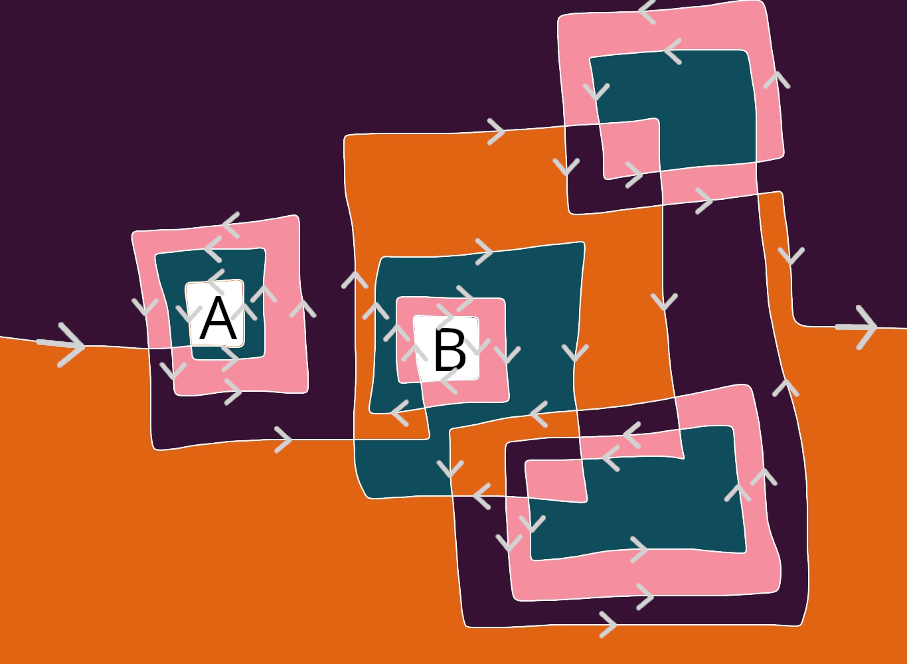
On remarque alors que si le turquoise est à droite d'une portion de la courbe blanche, alors l’orange est à gauche. Et si le rose est gauche, le violet est à droite. Du coup, la zone A est forcément orange et la zone B est violette.

Les zones sont en réalités colorées selon leur indice, c’est-à-dire en tenant compte du nombre de fois que la courbe blanche a tourné autour de chaque zone si on parcourt la courbe de gauche à droite. On tient aussi compte de l’orientation de la courbe – si on tourne dans le sens des aiguilles d’une montre ou pas. Comme il y a 4 couleurs, on compte tout cela modulo 4.

Cette image est issue d'une expérience collaborative ReShape par Hugo Parlier et Bruno Teheux.