Solution du défi
Choisis l'énigme dont tu veux voir une solution.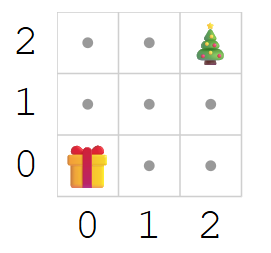
Explication 1:
Chemins possibles de 🎁 (0,0) à 🎄 (2,2)
Explication 2 :
Pourquoi y a-t-il exactement 6 chemins possibles ?
Pour compter le nombre de chemins allant de 🎁 (0,0) au 🎄 (2,2), on peut utiliser une méthode très efficace : numéroter chaque cellule par le nombre de façons d’y arriver. Cette méthode se base sur une idée simple :
➡️ de la cellule située à gauche (déplacement vers la droite)
⬆️ de la cellule située en dessous (déplacement vers le haut)
Donc : nombre de chemins pour arriver à cette cellule = somme des valeurs de ces deux cellules.
Remplissage de la grille
On commence par la première ligne et la première colonne :
- Le point de départ (0,0) vaut 1 : il y a exactement une façon d’y être.
- Sur une cellule de la ligne du bas, il n'est possible d'arriver que depuis la gauche → toutes les cellules valent 1.
- Sur une cellule de la colonne de gauche, il n'est possible d'arriver que depuis le bas → toutes les cellules valent 1.
Ensuite on remplit l’intérieur de la grille en appliquant la règle : gauche + bas.
| 0 | 1 | 2 | |
| y=2 | 1 | 3 | 6 |
| y=1 | 1 | 2 | 3 |
| y=0 | 1 | 1 | 1 |
Lecture de la dernière case
La case d’arrivée 🎄 est la case (2,2). Elle contient la valeur 6. Cela signifie que :
C’est précisément le nombre obtenu en listant tous les chemins comme dans l'explication 1. On peut aussi obtenir ce nombre en choisissant les façons d'ordonner 4 déplacements dont 2 sont vers la droite et 2 vers le haut.
- Images créées par l'auteur avec une IA et par programmation html.
- Texte révisé avec l'assistance d'une IA.
Explication :
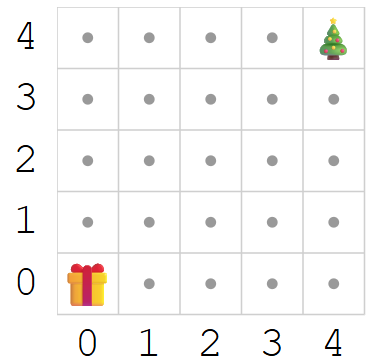
Pourquoi y a-t-il exactement 70 chemins possibles ?
Pour compter le nombre de chemins allant de 🎁 (0,0) au 🎄 (4,4), on utilise une méthode très efficace : numéroter chaque point par le nombre de façons d’y arriver. Cette méthode repose sur une idée très simple :
➡️ de la cellule située à gauche (déplacement vers la droite)
⬆️ de la cellule située en dessous (déplacement vers le haut)
Donc : nombre de chemins pour arriver à cette cellule = somme des valeurs de ces deux cellules.
Remplissage de la grille
On commence par la première ligne et la première colonne :
- Le point de départ (0,0) vaut 1 : il y a exactement une façon d’y être.
- Sur une cellule de la ligne du bas, il n'est possible d'arriver que depuis la gauche → toutes les cellules valent 1.
- Sur une cellule de la colonne de gauche, il n'est possible d'arriver que depuis le bas → toutes les cellules valent 1.
Ensuite, on remplit toute la grille en appliquant la règle : gauche + bas.
| 0 | 1 | 2 | 3 | 4 | |
| y=4 | 1 | 5 | 15 | 35 | 70 |
| y=3 | 1 | 4 | 10 | 20 | 35 |
| y=2 | 1 | 3 | 6 | 10 | 15 |
| y=1 | 1 | 2 | 3 | 4 | 5 |
| y=0 | 1 | 1 | 1 | 1 | 1 |
Lecture de la dernière case
La case d’arrivée 🎄 est la case (4,4). Elle contient la valeur 70. Cela signifie que :
Ce résultat correspond exactement au nombre de façons possibles d’ordonner 8 déplacements dont 4 vers la droite et 4 vers le haut.
- Images créées par l'auteur avec une IA et par programmation html.
- Texte révisé avec l'assistance d'une IA.
Explication 1 :
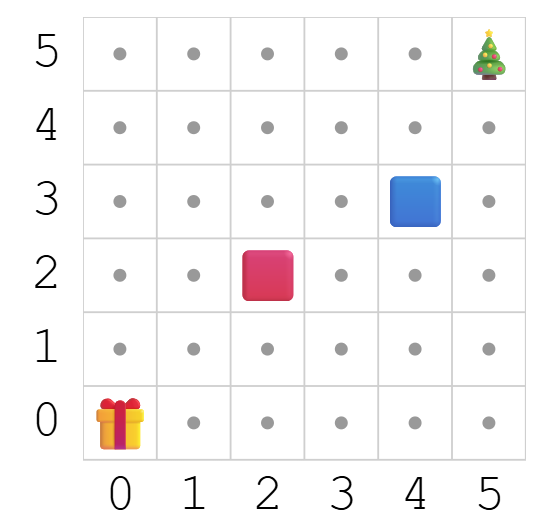
Comment obtenir le nombre total de chemins avec les deux piliers ?
Pour compter les chemins possibles que Volta 🤖 peut emprunter entre 🎁 (0,0) et 🎄 (5,5) tout en évitant les deux piliers 🟥 (2,2) et 🟦 (4,3), on utilise une méthode très efficace : numéroter chaque cellule par le nombre de façons d’y arriver.
Mais attention, les cellules occupées par les piliers restent vides, et on n’additionne pas à travers elles.
➡️ d’une cellule à gauche (c’est un déplacement vers la droite).
⬆️ d’une cellule en dessous (déplacement vers le haut).
Donc : Nombre de chemins = somme des valeurs de ces deux cellules.
⚠️ Exception : si la cellule est un pilier → elle reste vide, et aucun chemin ne peut y arriver ni en venir (on peut dire que sa valeur reste à 0).
Remplissage de la grille (avec obstacles)
On commence par la première ligne et la première colonne :
- Le point de départ (0,0) vaut 1 : il y a exactement une façon d’y être.
- Sur une cellule de la ligne du bas, il n'est possible d'arriver que depuis la gauche → toutes les cellules valent 1.
- Sur une cellule de la colonne de gauche, il n'est possible d'arriver que depuis le bas → toutes les cellules valent 1.
Ensuite on remplit l’intérieur de la grille en appliquant la règle : gauche + bas.
Voici la grille complète obtenue après application des règles. Les deux piliers 🟥 et 🟦 sont vides, et on ne peut ni y entrer, ni en sortir.
| 0 | 1 | 2 | 3 | 4 | 5 | |
| y=5 | 1 | 6 | 15 | 32 | 49 | 81 |
| y=4 | 1 | 5 | 9 | 17 | 17 | 32 |
| y=3 | 1 | 4 | 4 | 8 | 🟦 | 15 |
| y=2 | 1 | 3 | 🟥 | 4 | 9 | 15 |
| y=1 | 1 | 2 | 3 | 4 | 5 | 6 |
| y=0 | 1 | 1 | 1 | 1 | 1 | 1 |
Lecture de la dernière case
La case d’arrivée 🎄 est la case (5,5). Elle contient la valeur 81. Cela signifie que :
Cette méthode permet d’obtenir exactement le même résultat que le calcul combinatoire plus avancé (explication suivante), mais de manière visuelle et intuitive.
Explication 2 :
🧩 Premier élément d'analyse
Lorsqu’il n’y a aucun pilier, le robot Volta ne peut faire que deux types de mouvements :
- un pas vers la droite : D
- un pas vers le haut : H
Pour aller du départ \((0,0)\) à la case \((i,j)\), Volta doit faire \(i\) pas à droite et \(j\) pas en haut.
Il doit donc produire une suite de \(i+j\) mouvements contenant exactement \(i\) fois “droite” et \(j\) fois “haut”.
Le nombre de chemins possibles est simplement :
le nombre de façons de choisir où placer les \(j\) mouvements “haut” parmi les \(i+j\) mouvements totaux.
C’est exactement la définition du nombre de combinaisons, dont une des notations est :
\[ \binom{i+j}{j} \]
La formule de l'explication précédente :
\[ \text{valeur}(i,j) = \text{valeur}(i-1,j) + \text{valeur}(i,j-1) \]
correspond exactement à :
\[ \binom{i+j}{j} = \binom{i+j-1}{j} + \binom{i+j-1}{j-1} \]
… qui est l’identité fondamentale du triangle de Pascal.
1️⃣ Trajectoires totales sans obstacles
Déplacements : 5 à droite + 5 en haut → total 10 mouvements \[ \text{Trajectoires totales} = \binom{10}{5} = 252 \] ---2️⃣ Trajectoires passant par P1
- Départ → P1 (2,2) :
- Droite : 2, Haut : 2 → \(\binom{2+2}{2} = \binom{4}{2} = 6\)
- P1 → arrivée (5,5) :
- Droite : 5-2=3, Haut : 5-2=3 → \(\binom{6}{3} = 20\)
- Total passant par P1 : (6 × 20 = 120)
3️⃣ Trajectoires passant par P2
- Départ → P2 (4,3) :
- Droite : 4, Haut : 3 → \(\binom{7}{4} = 35\)
- P2 → arrivée (5,5) :
- Droite : 5-4=1, Haut : 5-3=2 → \(\binom{3}{1} = 3\)
- Total passant par P2 : (35 × 3 = 105)
4️⃣ Trajectoires passant par les deux piliers P1 puis P2
- Départ → P1 (2,2) : \(\binom{4}{2} = 6\)
- P1 → P2 :
- Droite : 4-2=2, Haut : 3-2=1 → \(\binom{3}{2} = 3\)
- P2 → arrivée : \(\binom{(5-4)+(5-3)}{1} = \binom{3}{1} = 3\)
- Total passant par les deux : (6 × 3 × 3 = 54)
5️⃣ Principe d’inclusion-exclusion
\[ \text{Trajectoires autorisées} = \text{Total} - (\text{P1 seules} + \text{P2 seules} - \text{P1 et P2}) \]- P1 seules = trajectoires passant par P1 mais pas P2 : (120 - 54 = 66)
- P2 seules = trajectoires passant par P2 mais pas P1 : (105 - 54 = 51)
- Les deux : 54
- Images créées par l'auteur avec une IA et par programmation html.
- Texte révisé avec l'assistance d'une IA.
Retour au calendrier.